- Worksheets
- Games
- Lesson Plans
- Workbooks
- Exercises
- Science Projects
- Skills Progression
- More
Search Equivalent Fraction Educational Resources
99 filtered results
99 filtered results
Equivalent Fractions
Sort by

Fractions 4
Guided Lesson
Fractions 4
Students are going to take a deeper dive into fractions in this unit! Learners will apply previous understanding of finding equivalent fractions, and converting between fractions and mixed numbers to work with fractions in more complex ways. Students will continue to use visual models to learn and practice adding, subtracting, multiplying and dividing fractions.
5th grade
Math
Guided Lesson

Fractions 1
Guided Lesson
Fractions 1
Fractions can be a tricky concept for third graders to master, but this guided lesson can help kids get there. It provides focused instruction designed by teachers and curriculum experts that is specific to the third grade curriculum. Exercises and practical examples help kids to put fractions in context with real-world math problems. When finished with the lesson, check out our fractions worksheets for more practice.
3rd grade
Math
Guided Lesson

Fractions 2
Guided Lesson
Fractions 2
Students will have a basic understanding of fractions coming into 4th grade. In this unit students will get to explore new ways of representing fractions, including in a set of data, on number lines and using area models. Students will use their knowledge of fractions to compare fractions with like and unlike denominators.
4th grade
Math
Guided Lesson

Fractions 3
Guided Lesson
Fractions 3
Fractions can be challenging when taught in an abstract way. That’s why this unit invites learners to engage with fractions and mixed numbers in very visual and concrete ways using number lines, tape diagrams and area models. Students will learn different strategies to practice identifying and generating equivalent fractions.
5th grade
Math
Guided Lesson
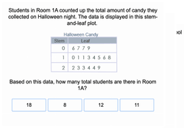
Measurement and Data 4
Guided Lesson
Measurement and Data 4
Representing data on graphs makes math visual and involves some creativity and design. Plotting data using fractional units takes their learning one step further. Also in this unit, students learn to measure using both traditional units (like inches, feet and yards) and metric units, and how to convert measurements within each system. The concept of measurement gets two dimensional when students explore measuring and working with angles.
4th grade
Math
Guided Lesson

Fifth Grade Fall Review Packet - Week 2
Workbook
Fifth Grade Fall Review Packet - Week 2
Prepare learners for their fifth grade debut with Week 2 of our Fifth Grade Fall Review Packet, complete with five more days of engaging activities that will review key skills and concepts.
5th grade
Reading & Writing
Workbook